Az elektromos tÃķltÃĐst leÃrÃģ fizikai mennyisÃĐg elÅjeles, skalÃĄris mennyisÃĐg.
Jele: Q,mÃĐrtÃĐkegysÃĐge a coulomb, a jele C (coulomb), 1C (coulomb) = 1 As
|
ÃramfajtÃĄk:
EgyenÃĄram: (angolul: Direct Current/DC)
Az elektromos ÃĄramot akkor nevezzÞk egyenÃĄramnak, ha az ÃĄramkÃķrben a tÃķltÃĐshordozÃģk ÃĄllandÃģ vagy vÃĄltozÃģ mennyisÃĐgben, de egyazon irÃĄnyban haladnak. Jele: =
VÃĄltakozÃģ ÃĄram: (angolul: Alternating Current/AC)
Az olyan villamos ÃĄramot, amelynek erÅssÃĐge ÃĐs irÃĄnya periodikusan vÃĄltozik, vÃĄltakozÃģÃĄramnak nevezzÞk. Jele: ~
|
FeszÞltsÃĐg:
Az elektromos tÃĐr egy adott pontjÃĄhoz viszonyÃtott munkavÃĐgzÅ kÃĐpessÃĐget potenciÃĄlnak, kÃĐt pont munkavÃĐgzÅ kÃĐpessÃĐgÃĐnek kÞlÃķnbsÃĐgÃĐt potenciÃĄlkÞlÃķnbsÃĐgnek vagy feszÞltsÃĐgnek nevezzÞk.
Az elektromos feszÞltsÃĐg vagy potenciÃĄlkÞlÃķnbsÃĐg jele: U, mÃĐrtÃĐkegysÃĐge a volt, amelynek a jele: V (volt).
1 V olyan vezetÅ kÃĐt pontja kÃķzÃķtti elektromos feszÞltsÃĐg, amelyben 1 A ÃĄllandÃģ erÅssÃĐgÅą ÃĄram folyik, ha az ÃĄram teljesÃtmÃĐnye e kÃĐt pont kÃķzÃķtt 1 W.
|
Ohm tÃķrvÃĐny:
Ohm tÃķrvÃĐnye kimondja, hogy a vezetÅn keresztÞl folyÃģ ÃĄram mÃĐrtÃĐke egyenesen arÃĄnyos a feszÞltsÃĐggel, ÃĐs fordÃtottan arÃĄnyos a vezetÅ ellenÃĄllÃĄsÃĄval.
Az arÃĄnyossÃĄgi tÃĐnyezÅ maga az ellenÃĄllÃĄs, melyet hasonlÃthatnÃĄnk a kÃķzegellenÃĄllÃĄshoz is. MinÃĐl nagyobb az ellenÃĄllÃĄs, annÃĄl kisebb lesz a lÃĐtrejÃķvÅ ÃĄramerÅssÃĐg, ÃĐs minÃĐl kisebb az ellenÃĄllÃĄs, annÃĄl nagyobb lesz a keletkezÅ ÃĄram, hiszen a tÃķltÃĐshordozÃģk mozgÃĄsa kevÃĐsbÃĐ akadÃĄlyozott.
MÃĄskÃĐpp megfogalmazva: egy fogyasztÃģ kÃĐt kivezetÃĐse kÃķzt mÃĐrhetÅ feszÞltsÃĐg ÃĐs a fogyasztÃģn ÃĄthaladÃģ ÃĄram erÅssÃĐge kÃķzÃķtt egyenes arÃĄnyossÃĄg van.
Az ellenÃĄllÃĄs jele: R, mÃĐrtÃĐkegysÃĐge az ohm, melynek a jele: âĶ (omega).
R= U
I
|
 |
|
/ IdeÃĄlis esetben, amikor nincs vezetÃĐk, ÃĐs generÃĄtor belsÅ ellenÃĄllÃĄs... /
UR = 12V
IR = 0.2A /200mA/
R = ?
R= Ur = 12V = 60 Ω
Ir 0.2A
|
Kirchhoff I: (csomÃģponti tÃķrvÃĐny)
PÃĄrhuzamosasn elÃĄgazÃģ ÃĄramkÃķrben a csomÃģpontba befolyÃģ ÃĄramerÅssÃĐgek Ãķsszege megegyezik a csomÃģpontot elhagyÃģ ÃĄramerÅssÃĐgek ÃķsszegÃĐvel.
I = I1 + I2 + I3 + Ix...
|
 |
 |
|
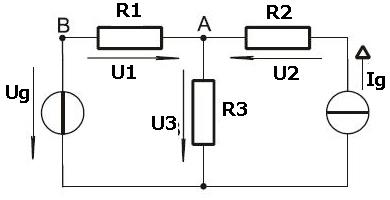
Egy csomÃģpontba befolyÃģ ÃĐs kifolyÃģ ÃĄramok:
I1 + I2 - I3 - I4 - I5 = 0
Ãtrendezve:
I1 + I2 = I3 + I4 + I5
IR1 = 1A
IR2 = 1A
IR3 = ?
A kÃĐpen lÃĄthatÃģ hogy IR1 ÃĐs IR2 befolyÃģ ÃĄram, akkor IR3 kifolyÃģ ÃĄram lesz.
IR3 = IR1 + IR2 = 1A +1A = 2A |
Kirchhoff II: (hurok tÃķrvÃĐny)
BÃĄrmely zÃĄrt hurokban az ÃĄramkÃķri elemeken lÃĐvÅ feszÞltsÃĐgek elÅjeles Ãķsszege nulla. |

Egy Ãķsszetett ÃĄramkÃķrbÅl kiemelt hurok |
VÃĄlasszunk a pÃĐldakÃĐnt szereplÅ hurokban egy kiindulÃģ csomÃģpontot, A-t ÃĐs egy kÃķrÞljÃĄrÃĄsi irÃĄnyt, pÃĐldÃĄul az ÃģramutatÃģ jÃĄrÃĄsÃĄnak megfelelÅen! Az A csomÃģpontbÃģl kiindulva, ÃĐs a vÃĄlasztott kÃķrÞljÃĄrÃĄssal egyezÅ irÃĄnyÚ feszÞltsÃĐgeket pozitÃvnak vÃĐve ÃrhatÃģ:
U1 + U2 - U3 + U4 - U5 = 0
U1 = 5V
U2 = 4V
U3 = 2V
U4 = 3V
U5 = ?
U1 + U2 - U3 + U4 - U5 = 0 EbbÅl: U1 + U2 - U3 + U4 = U5 EbbÅl: 5V + 4V - 2V + 3V = U5 ==> 10 = U5
|
KÃĐtpÃģlus soros kapcsolÃĄsa:
Azt mondjuk, hogy kÃĐt kÃĐtpÃģlus sorba van kapcsolva, ha egy-egy kivezetÃĐsÞkkel Ãķssze vannak kÃķtve.
KÃĐtpÃģlusnak a villamos hÃĄlÃģzatok kÃĐt kivezetÃĐssel rendelkezÅ elemeit nevezzÞk. |
 |
|
A soros kapcsolÃĄs egyik fÅ jellemzÅje az, hogy a sorba kapcsolt elemeken azonos ÃĄram folyik keresztÞl.
Az ÃĄbra jelÃķlÃĐseivel: Ig1 = Ig2
A soros kapcsolÃĄs mÃĄsik jellemzÅje az, hogy a sorosan kapcsolt elemeken az eredÅ feszÞltsÃĐget az elemeken esÅ rÃĐszfeszÞltsÃĐgek (elÅjelhelyes) ÃķsszegekÃĐnt szÃĄmÃthatjuk.
A kÃĐt generÃĄtor eredÅ feszÞltsÃĐge a huroktÃķrvÃĐny alapjÃĄn: UAB = Ug1 + Ug2
A kÃĐt feszÞltsÃĐggenerÃĄtort helyettesÃthetjÞk egyetlen eredÅ feszÞltsÃĐggenerÃĄtorral amelynek forrÃĄsfeszÞltsÃĐge a kÃĐt generÃĄtorfeszÞltsÃĐg Ãķsszege.
Uge = Ug1 + Ug2 |
KÃĐtpÃģlus pÃĄrhuzamos kapcsolÃĄsa:
Azt mondjuk, hogy kÃĐt kÃĐtpÃģlus pÃĄrhuzamosan van kapcsolva, ha mindkÃĐt kivezetÃĐsÞkkel Ãķssze vannak kÃķtve. Ha tÃķbb kÃĐtpÃģlus van mindkÃĐt kivezetÃĐsÃĐvel ÃķsszekÃķtve, akkor azt mondjuk, hogy mindegyik pÃĄrhuzamos kapcsolÃĄsban van egymÃĄssal. |
 |
|
PÃĄrhuzamosan kapcsolt elemeken a feszÞltsÃĐg azonos: U1 = U2
Ez belÃĄthatÃģ, ha a kÃĐt pÃĄrhuzamosan kapcsolt elem ÃĄltal alkotott hurokra alkalmazzuk Kirchoff huroktÃķrvÃĐnyÃĐt.
PÃĄrhuzamosan kapcsolt elemeken az eredÅ ÃĄramot az egyes ÃĄgak vagy ÃĄramÃĄnak elÅjelhelyes ÃķsszegekÃĐnt szÃĄmÃthatjuk: I = I1 + I2
Ez belÃĄthatÃģ, ha pl. a B csomÃģpontra pontra alkalmazzuk Kirchoff csomÃģponti tÃķrvÃĐnyÃĐt.
U1 = 12V
U2 = ?
I1 = 200mA
I2 = 2A
I = ?
U2 = U1 = 12V
I = I1 + I2 = 0.2A + 2A = 2.2A
|
EllenÃĄllÃĄsok soros kapcsolÃĄsa:
Ha nÃĐhÃĄny ellenÃĄllÃĄst sorbakÃķtÞnk, akkor a soros kapcsolÃĄs tulajdonsÃĄgai alapjÃĄn azt mondhatjuk, hogy:
|
 |
|
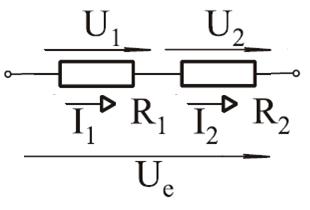
Az ellenÃĄllÃĄsokon ugyanakkora ÃĄram folyik ÃĄt: Ie = I1 = I2 ... = In
Az ellenÃĄllÃĄsokon esÅ feszÞltsÃĐg ÃķsszeadÃģdik: Ue = U1 + U2 ... + Un
Az ellenÃĄllÃĄsok ÃĐrtÃĐke ÃķsszeadÃģdik: Re = R1 + R2 ... + Rn
R1 = 150Ω
U1 = 30V
U2 = 60V
R2 = ?
Ie = I1 = I2 = U1 = 30V = 0.2A
R1 150Ω
R2 = U2 = 60V = 300Ω
I2 0.2A |
EllenÃĄllÃĄsok pÃĄrhuzamos kapcsolÃĄsa:
PÃĄrhuzamosan kapcsolt ellenÃĄllÃĄsok is helyettesÃthetÅk egyetlen eredÅ ellenÃĄllÃĄssal.
|
 |
|
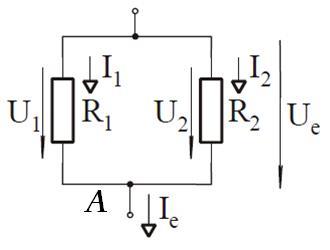
Kirchhoff csomÃģponti tÃķrvÃĐnye A csomÃģpontra: Ie = I1 + I2
Kirchhoff huroktÃķrvÃĐnye szerint a kÃĐtpÃģluson esÅ feszÞltsÃĐg azonos: Ue = U1 = U2
Az Re ellenÃĄllÃĄs ÃĐrtÃĐke:
Re = R1 * R2
R1 + R2
R1 = 220Ω
R2 = 470Ω
Re = ?
Re = R1 * R2 = 220Ω * 470Ω = 149.85Ω
R1 + R2 220Ω + 470Ω |
FeszÞltsÃĐgosztÃģ:
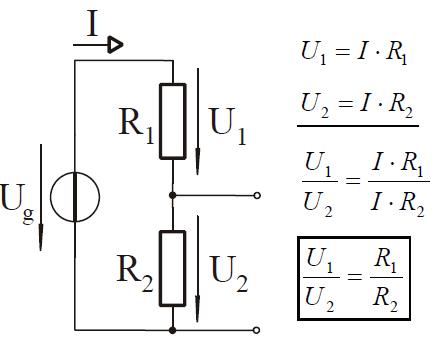
KÃĐt ellenÃĄllÃĄs sorba kapcsolÃĄsÃĄval feszÞltsÃĐgosztÃģt alakÃthatunk ki. |
 |
|
A tÃĄplÃĄlÃģ feszÞltsÃĐg megoszlik az R1 ÃĐs R2 ellenÃĄllÃĄsok kÃķzÃķtt, innen szÃĄrmazik a feszÞltsÃĐgosztÃģ elnevezÃĐs. FeszÞltsÃĐgosztÃģban a feszÞltsÃĐg az ellenÃĄllÃĄsokkal egyenes arÃĄnyban oszlik meg.
Ug = 30V
R1 = 100Ω
R2 = 200Ω
U2 = ?
I = Ug = 30v = 0.1A
R1 + R2 100Ω + 200Ω
U2 = I * R2 = 0.1A * 200Ω = 20V |
Lenz tÃķrvÃĐny:
Ha a vezetÅ hurokban vagy tekercsben feszÞltsÃĐg indukÃĄlÃģdott, akkor a hurokban ÃĄram folyik. Az indukÃĄlt feszÞltsÃĐg irÃĄnya mindig olyan, hogy ztÃĄrt vezetÅben az ÃĄltala lÃĐtrehozott ÃĄram kÃķrÞl keletkezÅ mÃĄgneses terÃĐvel akadÃĄlyozni igyekszik az Åt lÃĐtrehozÃģ indukÃĄlÃģ folyamatot. |
U = -N * dΦ
dt
|
|
U : indukÃĄlt feszÞltsÃĐg
N : tekercs menetszÃĄma
dΦ/dt : a mÃĄgneses tÃĐr fluxusÃĄnak vÃĄltozÃĄsi sebessÃĐge |
|

